Many statistical analysis problems involve categorical data in which observations belong to one of number of groups that have no numerical relationship between them. For example, male or female, nationality, what state a person is from, and the all time favorite of statistics textbooks, the 6 (or more) sides of a die. In this type of data, one group cannot be interpreted numerically as higher or lower than any other, but rather each group is equivalent to any other group, and membership in that group is what we’re interested in. While the 6 sides of a die have a numerical interpretation, each has an equal probability of occurring during any given roll, assuming the die is fair. Or so you would hope.
In my Categorical Data Analysis class, we explored this very assumption and looked at a paper by Karl Pearson from 1900 – On the Criterion that a Given System of Deviations from the Probable in the Case of a Correlated System of Variables is such that it Can Reasonably Be Supposed to have Arisen from Random Sampling. Very exciting, just from the title, isn’t it?? (More on that later.) In this paper, Pearson looked at a dataset (from a Professor W.F.R. Weldon) consisting of 26,306 rolls of 12 dice, and specifically “…the observed frequency of dice with 5 or 6 points…”
Seems simple enough. We can easily simulate 26,306 rolls of 12 dice and count the number of 5s or 6s. The observed data is added in, below, and we can compute the theoretical distribution of values using a Binomial Distribution in which we have 12 trials and the probability of success on any given trial is 1/3; 12 dice, count 5s or 6s.
> # simulate the 12-dice experiment > count <- factor(replicate(26306, length(which(sample(6, 12, replace=TRUE) >= 5))), + levels=0:12) > df <- as.data.frame(table(count)) > df$Prob <- round(df$Freq/26306, 4) > # add in the data from Pearson's paper > df$PearsonFreq <- c(185, 1149, 3265, 5475, 6114, 5194, 3067, 1331, 403, 105, 14, 4, 0) > df$PearsonProb <- round(df$PearsonFreq/26306, 4) > # include the expected distribution from the Binomial Distribution > bin <- dbinom(0:12, size = 12, prob = 1/3) > df$BinomialFreq <- as.integer(bin*26306) > df$BinomialProb <- round(bin,4) > df count Freq Prob PearsonFreq PearsonProb BinomialFreq BinomialProb 1 0 206 0.0078 185 0.0070 202 0.0077 2 1 1180 0.0449 1149 0.0437 1216 0.0462 3 2 3289 0.1250 3265 0.1241 3345 0.1272 4 3 5565 0.2115 5475 0.2081 5575 0.2120 5 4 6221 0.2365 6114 0.2324 6272 0.2384 6 5 5101 0.1939 5194 0.1974 5018 0.1908 7 6 2979 0.1132 3067 0.1166 2927 0.1113 8 7 1278 0.0486 1331 0.0506 1254 0.0477 9 8 375 0.0143 403 0.0153 392 0.0149 10 9 97 0.0037 105 0.0040 87 0.0033 11 10 12 0.0005 14 0.0005 13 0.0005 12 11 3 0.0001 4 0.0002 1 0.0000 13 12 0 0.0000 0 0.0000 0 0.0000 >
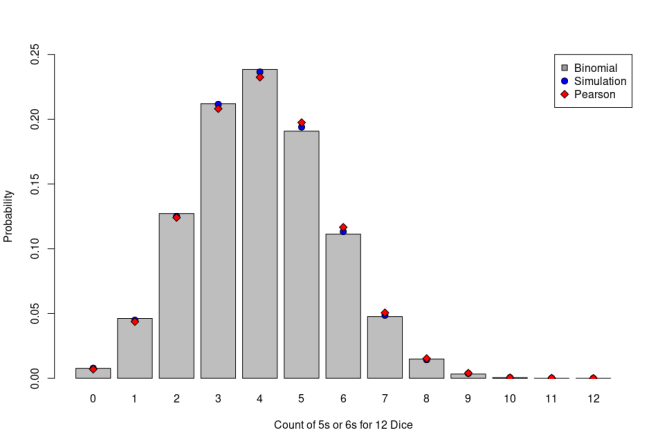
The numbers seem very close, but Pearson’s set shows consistently lower probabilities on the low side (0 through 5 counts of 5s or 6s) and consistently higher probabilities on the high side (6 through 9, and 11). Let’s look at that graphically. In the figure below, I’ve plotted the theoretical results from the Binomial Distribution as grey bars, results from my simulation as blue circles, and the probabilities from Pearson’s dice data as red diamonds. Visually the simulation seems closer to the theoretical result from the Binomial Distribution while the data from Pearson’s paper still seems to exhibit a bias. To be sure, we need to apply a statistical test.
For that statistical test, I refer back to Pearson’s paper from 1900 which actually introduced something that statisticians and data scientists use extensively – the Chi-squared Test. In fact, Pearson’s paper is considered to be one of the foundations of modern statistics and introduced the Chi-squared distribution as an alternative to the Normal Distribution which Pearson felt was being used in cases when it did not fit the data. Here I apply the Chi-squared test to these data in order evaluate the goodness of fit of the simulated or observed data to the expected distribution of observed 5s or 6s, assuming the dice are fair.
> # test the simulation for goodness of fit to the theoretical Binomial Distribution > chisq.test(df$Freq, p=dbinom(0:12, size=12, prob=1/3)) Chi-squared test for given probabilities data: df$Freq X-squared = 17.172, df = 12, p-value = 0.1432
> # test the observed dice data > chisq.test(df$PearsonFreq, p=dbinom(0:12, size=12, prob=1/3)) Chi-squared test for given probabilities data: df$PearsonFreq X-squared = 41.312, df = 12, p-value = 4.345e-05
The simulation seems to fit, but the observations certainly do not, given a p-value of .00004345! Clearly the observed dice are not fair based upon these observations and this would surely be of interest to a casino or anyone else depending upon the equal probability of any number occurring during any given roll.
The fascinating explanation for this experiment is actually a physical one. Consider the typical die composed of a uniform material into which the pips are drilled – in other words, material is removed to make the pips. The sides of the die are arranged such that opposite sides sum to 7 – 6 pips are opposite 1 pip, 5 pips are opposite 2 pips, and 4 pips are opposite 3 pips. As a result of this arrangement, 5 and 6 are adjacent to each other while 1 and 2 are adjacent to each other and on opposite sides to 5 and 6. This leads to the center of gravity of the die being shifted very sightly away from the sides with 5 and 6 pips leading to a very slight bias for a 5 or a 6 to land upward. Pearson’s Chi-squared test gives us the necessary tools to identify this bias – along with a very large collection of data.
26,306 actual rolls of 12 dice? It took about 1 second to simulate that on my laptop. How did they make the discoveries they did without computers?
*This blog post is based heavily on an exercise and discussion from my Categorical Data Analysis class. Seeing the application of this statistical test to identification of the physical bias that existed in the observed dice rolls inspired me to dig up Pearson’s paper and is certainly one of the best moments of my statistical training thus far. Thank you Dr. Breidt for that discussion and the inspiration.